Hukum Gerakan Planet Kepler
Di dalam astronomi, tiga Hukum Gerakan Planet Kepler adalah
- Setiap planet bergerak dengan lintasan elips, matahari berada di salah satu fokusnya.
- Luas daerah yang disapu pada selang waktu yang sama akan selalu sama.
- Perioda kuadrat suatu planet berbanding dengan pangkat tiga jarak rata-ratanya dari matahari.
Ketiga hukum diatas ditemukan oleh ahli matematika and astronomi jerman Johannes Kepler (1571–1630), yang menjelaskan gerakan planet di dalam tata surya. Hukum diatas menjabarkan gerakan dua benda yang saling mengorbit.
Karya Kepler didasari oleh data observasi Tycho Brahe, yang diterbitkannya sebagai 'Rudolphine tables'. Sekitar tahun 1605 Kepler menyimpulkan bahwa data posisi planet hasil observasi Brahe mengikuti rumusan matematika cukup sederhana yang tercantum diatas.
Hukum Kepler mempertanyakan kebenaran astronomi dan fisika warisan zaman Aristoteles dan Ptolemaeus. Ungkapan Kepler bahwa Bumi beredear sekeliling, berbentuk elips dan bukannya epicycle, dan membuktikan bahwa kecepatan gerak planet bervariasi, merubah astronomi dan fisika. Hampir seabad kemudian Isaac Newton mendeduksi Hukum Kepler dari rumusan hukum karyanya, hukum gerak dan hukum gravitasi Newton, dengan menggunakan Euclidean geometry klasik.
Pada era modern, hukum kepler digunakan untuk aproximasi orbit satelit dan benda-benda yang mengorbit matahari. Yang semuanya belum ditemukan pada saat Kepler hidup. (contoh: planet luar dan asteroid) Hukum ini kemudian diaplikasikan untuk semua benda kecil yang mengorbit benda lain yang jauh lebih besar, walaupun beberapa aspek seperti gesekan atmosfer (contoh: gerakan di orbit rendah), atau relativitas (contoh: prosesi preihelion merkurius), dan keberadaan benda lainnya dapat membuat hasil hitungan tidak akurat dalam berbagai keperluan.
Introduksi Tiga Hukum Kepler
Hukum hukum ini menjabarkan gerakan dua badan yang mengorbit satu sama lainnya. Masa dari kedua badan ini bisa hampir sama, sebagai contoh Charon—Pluto (~1:10), proporsi yang kecil, sebagain contol. Bulan—Bumi(~1:100), atau perbandingan proporsi yang besar, sebagai contoh Merkurius—Matahari (~1:10,000,000).
Dalam semua contoh diatas kedua badan mengorbit mengelilingi satu pusat masa, barycenter, tidak satupun berdiri secara sepenuhnya di atas fokus elips. Namun kedua orbit itu adalah elips dengan satu titik fokus di barycenter. Jika ratio masanya besar, sebagai contoh planet mengelilingi matahari, barycenternya terletak jauh di tengah obyek yang besar, dekat di titik masanya. Di dalam contoh ini, perlu digunakan instrumen presisi canggih untuk mendeteksi pemisahan barycenter dari titik masa benda yang lebih besar. Jadi, hukum Kepler pertama secara akurat menjabarkan orbit sebuah planet mengelilingi matahari.
Karena Kepler menulis hukumnya untuk aplikasi orbit planet dan matahari, dan tidak mengenal generalitas hukumnya, artikel wikini ini hanya akan mendiskusikan hukum diatas sehubingan dengan matahari dan planet-planetnya.
Hukum I Kepler
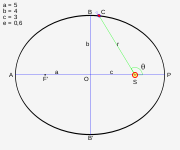
- "Setiap planet bergerak dengan lintasan elips, matahari berada di salah satu fokusnya."
Pada zaman Kepler, klaim diatas adalah radikal. Kepercayaan yang berlaku (terutama yang berbasis teori epicycle) adalah bahwa orbit harus didasari lingkaran sempurna. Pengamatan ini sangat penting pada saat itu karena mendukung pandangan alam semesta menurut Kopernikus. Ini tidak berarti ia kehilangan relevansi dalam konteks yang lebih modern.
Meski secara teknis elips yang tidak sama dengan lingkaran, tetapi sebagian besar planet planet mengikuti orbit yang bereksentrisitas rendah, jadi secara kasar bisa dibilang mengaproximasi lingkaran. Jadi, kalau ditilik dari observasi jalan edaran planet, tidak jelas kalau orbit sebuah planet adalah elips. Namun, dari bukti perhitungan Kepler, orbit orbit itu adalah elips, yang juga memeperbolehkan benda-benda angkasa yang jauh dari matahari untuk memiliki orbit elips. Benda-benda angkasa ini tentunya sudah banyak dicatat oleh ahli astronomi, seperti komet dan asteroid. Sebagai contoh Pluto, yang diobservasi pada akhir tahun 1930, terutama terlambat diketemukan karena bentuk orbitnya yang sangat elipse dan kecil ukurannya.
Hukum II Kepler
- "Luas daerah yang disapu pada selang waktu yang sama akan selalu sama."
Secara matematis:
dimana 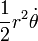 adalah "areal velocity".
adalah "areal velocity".
Hukum III Kepler
Planet yang terletak jauh dari matahari memiliki perioda orbit yang lebih panjang dari planet yang dekat letaknya. Hukum Kepelr ketiga menjabarkan hal tersebut secara kuantitativ.
- "Perioda kuadrat suatu planet berbanding dengan pangkat tiga jarak rata-ratanya dari matahari."
Secara matematis:
dimana P adalah period orbit planet dan a adalah axis semimajor orbitnya.
Konstant proporsionalitasnya adalah semua sama untuk planet yang mengedar matahari.


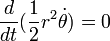
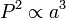


Tidak ada komentar:
Posting Komentar